Do the Wave: Trigonometry Comes Alive with Sketchpad
Do the Wave: Trigonometry Comes Alive with Sketchpad
2008 NCTM Annual Meeting
Session 335 Friday, April 11 8:00am
Scott Steketee, Key Curriculum Press, stek@keypress.com
Summary
Trigonometry makes sense and is more fun when students make sinusoids actually wave, combine the waves, and explore real-world applications. As you look at these activities, consider how they can be used to improve student understanding. To draw attention to particular instructional strategies that are valuable when using these activities, each activity's description is followed by a question about using a specific strategy in conjunction with the activity. (There's also a longer list of useful strategies and a bibliography of useful references.)
Objectives
- Encourage the use of dynamic math software to enliven the study of sinusoids in trigonometry.
- Show ways to present and study this topic in a way that allows students to create and observe periodic motion.
- Include periodic motion examples from physics.
- Deepen student (and teacher) mathematical understanding of periodic motion and its applications.
- Consider how appropriate research-based instructional strategies can enhance these activities.
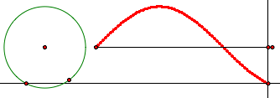 A Sine Wave Tracer
A Sine Wave Tracer
Students use compass and straightedge to construct a circle and a segment. They place points on these two objects, do a couple of simple constructions, and then animate the two points to create a sine wave. (This activity is suitable in a geometry course or at the beginning of a trig unit.)
Cooperative Learning: How can doing this activity in pairs or small groups increase its effectiveness?
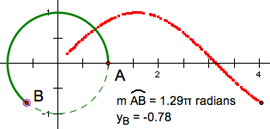 Unit Circle Functions
Unit Circle Functions
Students start with a point on a unit circle and make two measurements. Students observe the numeric values of the measurements and then plot the corresponding point to study how one measurement is a function of the other.
Pairs vs. Whole-Class: What are the advantages of using this activity with student pairs or with the whole class? In a whole-class presentation, what strategies can you use to maximize student involvement?
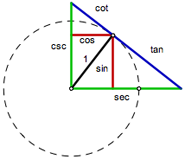 Six Circular Functions
Six Circular Functions
Students use a point on the unit circle to construct six segments that correspond to the six trig functions.
Multiple Representations: How can this activity help students relate the right-triangle and unit-circle representations of the trig functions?
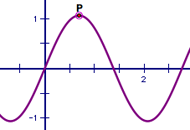 The Sine Challenge
The Sine Challenge
Given a coordinate system and a point, students are challenged to construct a sine function so that the first crest of the function passes through the point.
Generating and Testing Conjectures: As students try to solve this challenge, how can you encourage them to form and test conjectures in an organized way? How can you encourage students to think strategically without reducing the cognitive demand of the task?
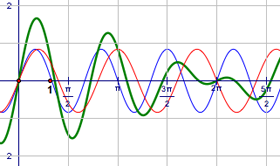 Sums of Sinusoidal Functions
Sums of Sinusoidal Functions
Students construct two sinusoids and their superposition and explore how the superposition depends on the amplitude, phase, and frequency of the two original sinusoids. They animate the phase of the original functions and explore how the superposition changes. Students explore how a sum of sine waves can produce a square wave, and manipulate sample sketches showing connections to light and sound.
Similarities and Differences: How can you use this activity to ask students to identify the similarities and differences between the various functions?
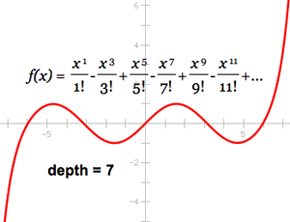 The Taylor Series
The Taylor Series
Students construct sums of polynomial functions and explore how increasing the number of terms in the sum can represent other functions with increasing accuracy. By using an iterative process students can change the number of terms used in the sum to see how the approximation changes as the number of terms increases.
Advance Cues:Before doing this activity, how can you activate students’ existing knowledge to prepare them to understand the relationship between polynomial and sinusoidal functions?
Tracing the Slope Function
Students construct a secant line on the graph of a sine function, measure the slope of the secant, and explore how the slope changes as the secant line moves along the graph.
Effective Questioning:As you do this presentation, what questions can you ask students, and what questioning behaviors can you employ, that will increase its effectiveness? How can you improve the quality of the discussion using wait time and revoicing?
Summarizing:How can you encourage students to summarize this activity and their understanding of the mathematics in it?
Reflection
How would you summarize these activities and suggestions? What did you find of value, and how might you use elements (activities, ideas, strategies) to benefit your own classes?
Permission
These activities are taken from various Sketchpad activity books, available at www.keypress.com/gspcurriculum. Key Curriculum Press grants teachers who attended this session the right to reproduce activities presented here for use with their own students. Other teachers can obtain the activities by purchasing the activity books. (Several activities are available as free samples; visit the web page for details.)
Research-Based Instructional Strategies
There are a number of research-based strategies that have been shown to increase student engagement with and understanding of the subject matter, in mathematics and in other subject areas. A few of them are summarized below. (Each strategy lists a source from the Bibliography. Consult these sources for suggestions about implementing the strategy and for information about the research that supports the strategy.)
- Wait Time: After you ask a question, give students plenty of time to understand it, consider it, and formulate a response. Allow a minimum of 3 to 5 seconds, or more for complex questions. (Springer & Dick)
- Revoicing: Repeat, summarize, or rephrase student contributions to a discussion to focus attention on what the student has said and to encourage further discussion. (Springer & Dick)
- Collective Reflection: Ask students to describe the problem-solving process in which they have engaged—what have they learned and how have they learned it? (Springer & Dick)
- Identifying Similarities and Differences: Ask students to describe similarities and differences between two different ways of solving the same problem or between two ways of representing the same mathematical concept. (Marzano)
- Summarizing and Note Taking: Have students summarize their findings at the end of an activity, preferably through both class discussion and written notes and answers. (Marzano)
- Reinforcing Effort and Providing Recognition: Look for opportunities to encourage student effort and point out the connection between effort and achievement. (Marzano)
- Multiple Representations: Expose students to a variety of representations of important mathematical concepts. Marzano emphasizes that some of the representations should be nonlinguistic—Sketchpad activities excel at making graphical representations accessible. Often students can recall a Sketchpad image to remind themselves of important concepts and methods. (Marzano)
- Cooperative Learning: Have students work in pairs or small groups. Use a variety of groupings, including both short-term and longer-term teams. (Marzano)
- Generating and Testing Hypotheses: Explicitly ask students to form and test conjectures, and encourage the process by affirming their efforts to form and express conjectures whether the actual conjectures are right or wrong. (Marzano)
- Cues and Questions: Remind students of what they know about a topic at the start of an activity. High-level questions produce deeper learning than recall or recognition questions. (Marzano)
- Appropriate Feedback: Provide feedback that’s corrective, timely, and specific to a criterion. The right kind of feedback has a powerful effect on student learning. Feedback that doesn’t depend on the teacher can be particularly effective. (Marzano)
- Formative Assessment and Self-Assessment: Use assessment to adapt your teaching to meet student needs. Such formative assessment produces substantial learning gains. Self-assessment helps students understand the purpose of their learning and what they can do to improve. (Black & William)
- Multiple Solutions: Take advantage of problems with multiple solutions. Problems with more than one route to a solution capture student interest and inspire mathematical thinking. (Kalman)
Bibliography for Instructional Strategies
The following books and articles can be very useful as you adapt the use of Sketchpad to your classroom and your teaching methods.
- Marzano, Robert J., Debra J. Pickering, and Jane E. Pollock. Classroom Instruction That Works. Association for Supervision and Curriculum Development, 2001. This book lists a number of effective classroom strategies, describes the research that supports them, and is full of practical suggestions for employing them in the classroom.
- Stein, Mary Kay, Margaret Schwan Smith, Marjorie A. Henningsen, and Edward A. Silver. Implementing Standards-Based Mathematics Instruction: A Casebook for Professional Development. NCTM, co-published with Teachers College Press, 2000. This book recommends classifying the mathematical tasks we set for students in terms of their cognitive demand, and provides a classification scheme with commentary and examples. It then provides detailed descriptions of a number of cases (situations in which a teacher sets up and implements a particular task for her middle school mathematics students) and analyzes those cases, looking at various teacher strategies and how they affected the maintenance of cognitive demand and what they implied for student learning.
- Driscoll, Mark. Fostering Algebraic Thinking: A Guide for Teachers of Grades 6–10. Heinemann, 1999. This book aims to provide teachers with strategies to help students build algebraic habits of mind. It addresses various broad topics in pre-algebra and algebra, describing obstacles in student thinking to be overcome, strategies for doing so, and lots of annotated examples.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, 2000.
- Springer, G. T., and Thomas Dick. “Making the Right (Discourse) Moves: Facilitating Discussions in the Mathematics Classroom.” Mathematics Teacher 100, no. 2 (September 2006), National Council of Teachers of Mathematics.
- Black, Paul and Dylan William, “Inside the Black Box: Raising Standards through Classroom Assessment.” Phi Delta Kappan 80, no. 2 (October 1998), Phi Delta Kappa International.
- Kalman, Richard, “The Value of Multiple Solutions.” Mathematics Teaching in the Middle School 10, no. 4 (November 2004), National Council of Teachers of Mathematics.