Half Plane Model of Hyperbolic Geometry

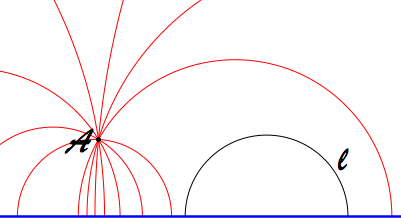
In the half-plane model of hyperbolic geometry, we consider points on one side of a horizontal boundary line. A "line" through two points in this model is a semicircle whose center is on the boundary line. A segment is an arc on that semicircle. If one point is directly above the other, the semicircle is replaced by a vertical ray with its endpoint on the boundary line.

The figure below shows a line CD and another line through point E, parallel to CD (i.e., the lines don't intersect). How many lines do you think there are through point E parallel to CD?

This Half-Plane Model of Hyperbolic Geometry sketch (by Judit Abardia Bochaca) depicts the hyperbolic plane and contains Custom Tools to create constructions in the upper half-plane. The Hyperbolic Triangles sketch depicts the same hyperbolic geometry model and contains Custom Tools for creating various centers of triangles constructed in the half-plane. Finally, the author's Hyperbolic Isometries sketch provides tools for constructing rotations, dilations, and translations in the half-plane model. Additional Catalan-language descriptions and a hyperbolic-geometry workshop guide are available here.

An earlier half-plane model, by Dan Bennett and referenced in Thomas Sibley's Instructor's Resource Guide for The Geometric Viewpoint (Addison Wesley, 1997), is available here.